Sequential Uniform Design
We advocate to reformulate AutoML as a kind of Computer Experiment for the purpose of maximizing ML prediction accuracy ([Yang2019]). Within Computer Experiment framework, we propose a novel SeqUD approach for algorithm selection and optimal hyperparameter configuration.
Motivation
Uniform design is a typical space-filling design for computer experiments, as proposed by [Fang1980] and [Wang1981]. It aims at scattering design points into the search space as evenly as possible, as shown in the figure below.

However, it is still a one-shot design method, which has similar limitations as grid search and random search. Accordingly, we develop a sequential uniform design method, which enjoys the advantage of both batch design and sequential strategy.
SeqUD Algorithm
Define the search space by converting individual hyperparameters (upon necessary transformation) into unit hypercube \(C = [0,1]^d\): linear mapping if continuous/integer-valued, one-hot encoding if categorical.
Start with a set of UD trials \(\theta \in C\) to evaluate ML model’s CV scores; find \(\hat\theta_0^*\).
Sequential refining strategy: for iterative step \(t=1,2,\ldots,T_{\max}\)
Centered at \(\hat\theta^*_{t-1}\), define the search subspace with reduced range and increased granularity.
Find augmented UD in the subspace; train ML algorithm with new \(\theta\) samples and obtain CV scores.
Collect all trained \(\{\theta, \mbox{CV}(\theta)\}\), and find \(\hat\theta_t^{*}\).
Output the optimal \(\theta^*\) from all trained \(\{\theta, \mbox{CV}(\theta)\}\).
Illustrative Demo
The figure below shows a two-stage example of the SeqUDHO approach in a 2-D space. The circle points represent the initial uniform design via \(U_{20}(20^{2})\). The surrounding box serves as the subspace of interest centered on the optimal trial \(x^{*}_{1}\) at the first stage, which is denoted by a square point in green. At the second stage, new trial points are augmented to form a \(U_{20}(20^{2})\), denoted by the blue triangle points.
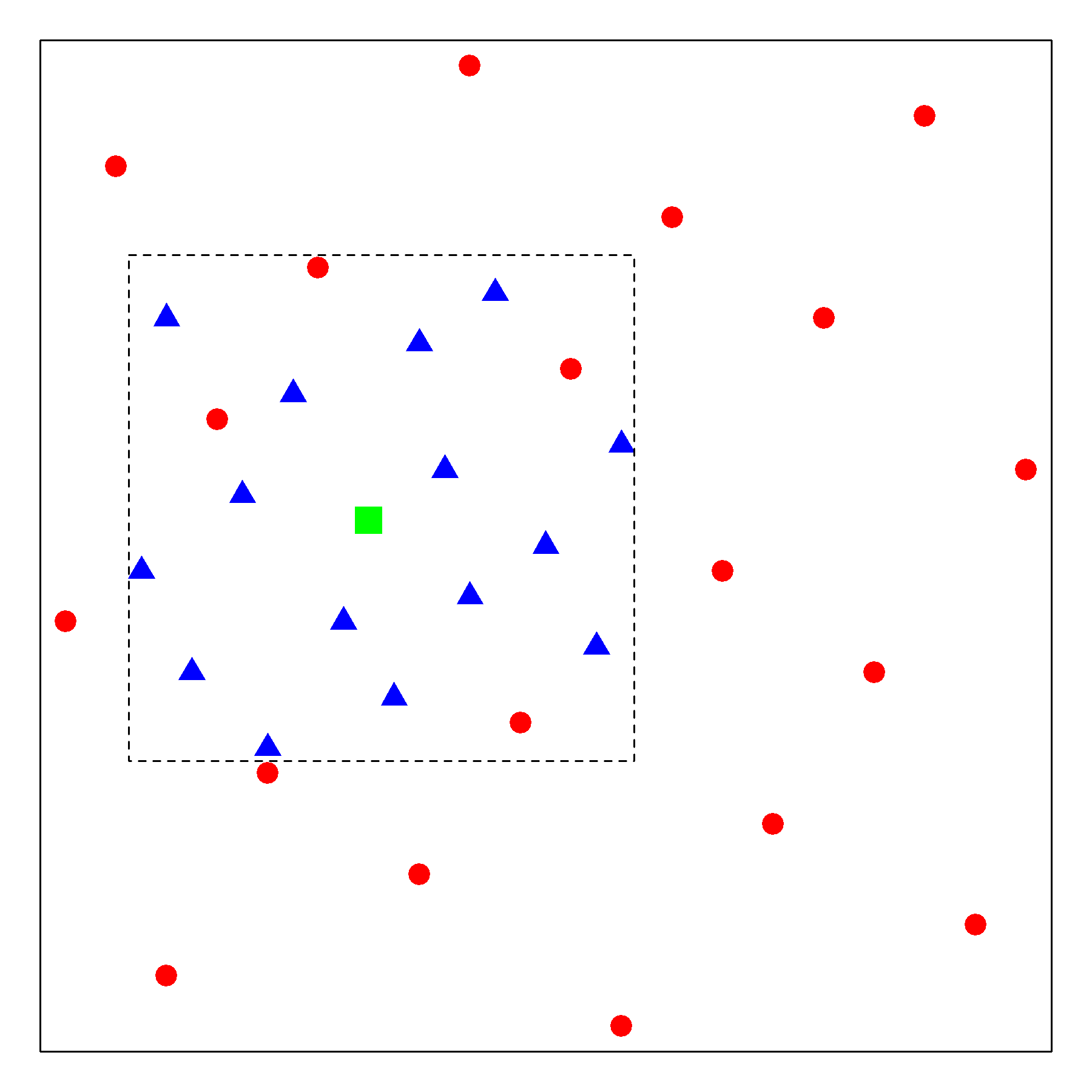
The proposed approach is advantageous over the Bayesian optimization methods.
Uniformly distributed trials can have a better exploration.
It is free from the meta-modeling and acquisition optimization.
At each stage, the algorithm could be conducted in parallel.
To generate such a augmented design, we have developed another package pyunidoe, which can be found in the git repository https://github.com/ZebinYang/pyunidoe.git.
Example Usage
SVM for Classification:
import numpy as np
from sklearn import svm
from sklearn import datasets
from matplotlib import pylab as plt
from sklearn.model_selection import KFold
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import cross_val_score
from sklearn.metrics import make_scorer, accuracy_score
from sequd import SeqUD
sx = MinMaxScaler()
dt = datasets.load_breast_cancer()
x = sx.fit_transform(dt.data)
y = dt.target
ParaSpace = {'C': {'Type': 'continuous', 'Range': [-6, 16], 'Wrapper': np.exp2},
'gamma': {'Type': 'continuous', 'Range': [-16, 6], 'Wrapper': np.exp2}}
estimator = svm.SVC()
score_metric = make_scorer(accuracy_score, True)
cv = KFold(n_splits=5, random_state=0, shuffle=True)
clf = SeqUD(ParaSpace, level_number=20, max_runs=100, max_search_iter=30, n_jobs=10,
estimator=estimator, cv=cv, refit=True, verbose=True)
clf.fit(x, y)
clf.plot_scores()